SISTEMAS DINÃMICOS GRACELI - DENTRO DO SISTEMA FÍSICO DE GRACELI QUE INCLUI ENTRE OUTROS, AS DIMENSÕES DE GRACELI, OS TENSORES, ENERGIAS, E OUTROS.

E QUE VARIA NO SISTEMA  MECÂNICO QUÂNTICO QUÍMICO RELATIVÍSITICO GRACELI.

Na física matemática e na matemática, sistema dinâmico é um conceito no qual uma função descreve a relação no tempo de um ponto em um espaço geométrico. Os exemplos incluem modelos matemáticos que descrevem o balanço do pêndulo do relógio, o fluxo de água em um duto, a relação entrada-saída de tensão em um circuito elétrico, a velocidade angular de saída de um motor, etc.

O conceito de sistema dinâmico nasce da exigência de construir um modelo geral para os sistemas físicos que evoluem no tempo, segundo uma regra que liga o estado presente aos estados passados. E SE TRATANDO DE SISTEMA DINÃMICOS GRACELI SE ENCONTRA E VARIA CONFORME  /G ψ = E ψ =  E [tG+].... ../ c .

História

Os primórdios da teoria dos sistemas dinâmicos podem ser identificados já no século XVI, nos trabalhos de mecânica celeste escritos por Johannes Kepler. As contribuições de Isaac Newton à modelagem matemática através da formalização da mecânica clássica abriram espaço para uma sofisticação crescente do aparato matemático que modela fenômenos mecânicos, culminando nos trabalhos de Lagrange e Hamilton, que definiram a teoria da mecânica clássica num contexto matemático, que essencialmente é o mesmo estudado até hoje.

O matemático francês Henri Poincaré é considerado um dos criadores da teoria moderna dos sistemas dinâmicos, tendo introduzido muitos dos aspectos do estudo qualitativo das equações diferenciais que permitiram estudar propriedades assintóticas das soluções (ou da maior parte das soluções) de uma equação diferencial, como estabilidade e periodicidade, sem ser necessário resolver explicitamente a equação diferencial. Tal abordagem pode ser encontrada na sua obra-prima Les méthodes nouvelles de la mécanique céleste, publicada em três volumes entre 1892 e 1899.

Considera-se que o primeiro livro publicado na área de sistemas dinâmicos é a obra Dynamical Systems, escrita pelo matemático estado-unidense George Birkhoff, e publicada em 1927.

Entre as ferramentas mais utilizadas na teoria dos sistemas dinâmicos estão a geometria diferencial, a teoria da medida e a geometria simplética.[2]

Definição

Sejam  um espaço topológico e  um semigrupo topológico.

Dizemos que um sistema dinâmico é um par  onde  é uma aplicação contínua que satisfaz:

•  se  e   E NO SISTEMA DINÂMICO GRACELI VARIA CONFORME  /G ψ = E ψ =  E [tG+].... ../ c .
• 
  
• e
•  onde  e  é o elemento neutro do grupo.

Um sistema dinâmico contínuo é um sistema dinâmico cujo estado evolui ao longo do espaço de estado continuamente de acordo com uma regra fixa.[1]

Usaremos a notação abreviada , ,  para representar as derivadas, em ordem ao tempo, de uma função  que depende do tempo, e , ,  para representar as derivadas de uma função  que depende de .

Consideremos, por exemplo:

POREM NO SISTEMA GRACELI FICA.:

 /G ψ = E ψ =  E [tG+].... ../ c 

Sistemas lineares

O movimento de um sistema linear invariante no tempo descrito pela quaterna (A,B,C,D) é dado pela fórmula de Lagrange:

 

/G ψ = E ψ =  E [tG+].... ../ c 

onde:

x(t) é o movimento do sistema

 é o movimento livre do sistema

 é o movimento forçado do sistema

 para sistemas a tempo continuo e  para sistemas a tempo discreto e se chama matriz de transição

 é a função de ingresso do sistema definida do intervalo [0,t)

 é 1 operador linear aplicado à função de ingresso

Um sistema linear é dito assimptoticamente estável quando:

 

/G ψ = E ψ =  E [tG+].... ../ c 

Ou seja o movimento livre do sistema tende a zero quando o tempo tende a infinito para toda condição inicial x(0). Isso só é possível se a matriz de transição tender a zero para o tempo tendente a infinito.

Na Teoria dos sistemas dinâmicos, um sistema é dito estruturalmente estável caso as propriedades topológicas do sistema dinâmico se mantenham as mesmas após uma pequena perturbação da transformação que define a dinâmica.

Definição

Um difeomorfismo de classe   definido sobre uma variedade suave  define um sistema dinâmico estruturalmente estável sobre  caso exista uma vizinhança  de f no espaço dos difeomorfismos de classe  sobre  (munido da topologia de Whitney), de forma que qualquer difeomorfismo  em  seja topologicamente equivalente a . De forma análoga, dizemos que  é estruturalmente estável.

O conceito de estabilidade estrutural se estende mutatis mutandis para fluxos.

POREM, NO SISTEMA DINÂMICO GRACELI VARIA NÃO APENAS NO TEMPO E ESPAÇO, MAS, TAMBÉM NA MECÂNICA DE GRACELI  REPRESENTADO POR :

/G ψ = E ψ =  E [tG+].... ../ c 

  MECÂNCIA GENERALIZADA GRACELI DE INTERAÇÕES E TRANSFORMAÇÕES.

LEI -

TODA INTERAÇÃO LEVA  A TRANSFORMAÇÕES, E VICE-VERSA.

INTERAÇÕES COMO E EM:

NAS INTERAÇÕES DAS FORÇAS FUNDAMENTIAS.

INTERAÇÕES DE SPIN - ÓRBITA.

ESTRUTURA - TEMPERATURA.

DISTRIBUIÇÃO ELETRÔNICA - NÍVEIS DE ENERGIA - BANDAS.

ELÉTRONS - FÓNOS.

ELÉTRONS - ELÉTRONS.

ESTADO QUÂNTICO - NÚMERO QUÃNTICO.

ENTROPIA -TEMPERATURA - MOVIMENTO BROWNIANO - CAMINHOS DE PARTÍCIULAS.

CATEGORIA - DIMENSÕES - FENÔMENOS [NO SISTEMA SDCTIE GRACELI].

ENTROPIA - ENTALPIA. ETC.

VEJAMOS AS INTERAÇÕES DE CAMPOS.

E EM RELAÇÃO AO SISTEMA  DE MECÂNICA GENERALIZADO GRACELI.

   eletromagnetismo quântico químico relativístico Graceli.

MECÂNICA DO SISTEMA DIMENSIONAL GRACELI.

ONDE A MAIORIA DOS FENÔMENOS FÍSICOS [EM TODAS AS ÁREAS] VARIAM CONFORME O SISTEMA DIMENSIONAL GRACELI.

SENDO ELE;

      EQUAÇÃO GERAL DE GRACELI.[quantização de Graceli].

  G ψ = E ψ = IGFF   E [tG+].... ..  =

G ψ = E ψ = IGFF  E [tG+]ψ ω /c] =   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   [ q G*]ψ μ / h/c ψ(x, t)  [x  t ]..

[ q [tG*] ==G ψ = E ψ = IGFF   E [tG+].... .. 

SISTEMA GRACELI DE:

 TENSOR [tG+] GRACELI = IGFF + SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO,  SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI. 

[ q [tG*] = energia quântica Graceli.

Força fundamental - INTERAÇÕES GRACELI IG =

IGFF = INTERAÇÕES GRACELI -  Força fundamental.

 T = TEMPERATURA.

PERMEABILIDADE MAGNÉTICA .

INTERAÇÃO SPINS ÓRBITA.

MOMENTUM MAGNÉTICO.

DISTRIBUIÇÃO ELETRÔNICA DOS ELEMENTOS QUÍMICOS.

NÍVEIS E SUBNIVEIS DE ENEREGIA.

BANDAS DE ENERGIAS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [1]

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ..  [2]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [-1]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ..  [-1]

RELATIVIDADE DAS FORÇAS FUNDAMENTAIS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. / c .

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =  E [tG+].... ../ c .

Em matemática e ciência física, harmónicos esféricos são funções harmónicas que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Os harmónicos esféricos são importantes em muitas aplicações teóricas e práticas, particularmente em física atómica (uma vez que a função de onda do electrão contém harmónicos esféricos) e na teoria do potencial, tanto no campo gravitacional como na eletrostática. 

SENDO QUE NO SISTEMA DE GRACELI NÃO APENAS VARIAM EM RELAÇÃO AO ESPAÇO E TEMPO, MAS TAMBÉM EM RELAÇÃO AO SISTEMA DIMENSIONAL DE GRACELI E A MECÃNICA QUÂNTICA QUÍMICA RELATIVISTA, VEJAMOS.:

Introdução

Harmónicos esféricos de variável real Y_lm, para l =0,...,4 (de cima para baixo) e m = 0,...,4 (da esquerda para a direita). Os harmónicos Y_l-m com m negativo são idênticos, mas com uma rotação de 90º/m em torno do eixo z em relação aos harmónicos positivos.

A equação de Laplace em coordenadas esféricas é dada por:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

/G ψ = E ψ =  E [tG+].... ../ c .

(Ver também Nabla e laplaciano em coordenadas esféricas). Se nesta expressão considera-se soluções específicas da forma ${\displaystyle f(r,\theta ,\phi )=R(r)Y(\theta ,\varphi )}$,/G ψ = E ψ =  E [tG+].... ../ c .

 a parte angular Y é chamada harmónico esférico e satisfaz a relação

${\displaystyle {1 \over \sin \theta }{d \over d\theta }\left(\sin \theta {dY(\theta ,\varphi ) \over d\theta }\right)+{1 \over \sin ^{2}\theta }{d^{2}Y(\theta ,\varphi ) \over d\varphi ^{2}}+l(l+1)Y(\theta ,\varphi )=0}$

/G ψ = E ψ =  E [tG+].... ../ c .

Se, por sua vez, utiliza-se o método de separação de variáveis para esta equação, pode-se ver que a equação acima admite soluções periódicas nas duas coordenadas angulares (l é um inteiro). Logo, a solução periódica do sistema anterior depende de dois inteiros (l, m) e é dada em termos de funções trigonométricas e dos polinômios associados de Legendre:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta })}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

Onde: ${\displaystyle Y_{\ell }^{m}}$ é chamada de função harmónica esférica de grau ${\displaystyle \ell }$ e ordem ${\displaystyle m}$; ${\displaystyle P_{\ell }^{m}}$ é o polinómio associado de Legendre; ${\displaystyle N}$ é uma constante de normalização; e ${\displaystyle \theta }$ e ${\displaystyle \varphi }$ representam os parâmetros angulares (respectivamente, o ângulo azimutal ou colatitude e o ângulo polar ou longitude).

As coordenadas esféricas utilizadas neste artigo são consistentes com àquelas usadas pelos físicos, mas diferem das utilizadas pelos matemáticos (ver coordenadas esféricas). Em particular, a colatitude ${\displaystyle \theta }$, ou ângulo polar, assume valores de ${\displaystyle 0\leq \theta \leq \pi }$ e a longitude ${\displaystyle \varphi }$, ou azimute, está na faixa de ${\displaystyle 0\leq \varphi <2\pi }$. Portanto, ${\displaystyle \theta }$ é nulo no Pólo Norte, ${\displaystyle \pi /2}$ no Equador e ${\displaystyle \pi }$ no Pólo Sul.

Quando a equação de Laplace é resolvida em coordenadas esféricas, as condições de periodicidade na fronteira da coordenada ${\displaystyle \varphi }$ e as condições de regularidades nos "Pólos Norte e sul" da esfera condizem com o que foi dito que os números l e m necessários devem ser inteiros que satisfazem ${\displaystyle \ell \geq 0}$ e ${\displaystyle |m|\leq \ell }$.

Normalização

Há várias normalizações utilizadas para as funções harmónicas esféricas. Em física e sismologia essas funções são geralmente definidas como

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=A_{\ell }^{m}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

onde

${\displaystyle A_{\ell }^{m}={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

Estas funções são ortonormalizadas,

${\displaystyle \int _{\varphi =0}^{2\pi }d\varphi \int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$,

/G ψ = E ψ =  E [tG+].... ../ c .

onde δ_aa = 1, δ_ab = 0 se a ≠ b (ver delta de Kronecker). Nas áreas de geodésia e análise espectral utiliza-se

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

que possui um termo linear

${\displaystyle {1 \over 4\pi }\int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$.

/G ψ = E ψ =  E [tG+].... ../ c .

No magnetismo, no entanto, usa-se os harmónicos de Schmidt semi-normalizados,

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {(\ell -m)! \over (\ell +m)!}}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

que possuem a seguinte normalização:

${\displaystyle \int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,={4\pi \over (2\ell +1)}\delta _{\ell \ell '}\,\delta _{mm'}}$.

/G ψ = E ψ =  E [tG+].... ../ c .

Utilizando a identidade (ver funções associadas de Legendre)

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}}$ 

/G ψ = E ψ =  E [tG+].... ../ c .

pode-se demonstrar que todas as funções harmónicas esféricas normalizadas acima satisfazem

${\displaystyle Y_{\ell }^{m*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi )}$, 

/G ψ = E ψ =  E [tG+].... ../ c .

onde o símbolo * significa conjugação complexa.

Convenção de fase de Condon-Shortley

Um forte motivo para uma confusão com a definição de harmónicos esféricos é o fator de fase ${\displaystyle (-1)^{m}\,}$, normalmente identificado como a fase de Condon-Shortley na literatura quântica. Na mecânica quântica, é uma prática usual incluir este fator de fase na definição das funções associadas de Legendre, ou anexá-lo à definição de funções harmónicas esféricas. Não há nenhuma exigência da utilização da fase de Condon-Shortley na definição de funções harmónicas esféricas, mas se ela for incluída, então algumas operações no domínio da mecânica quântica serão mais simples. No magnetismo e na geodésia, ao contrário, nunca incluiu-se o fator de fase Condon-Shortley na definição dos harmónicos esféricos.

Expansão em harmónicos esféricos

Os harmónicos esféricos formam um conjunto completo ortonormal de funções e, portanto, formam um espaço vetorial análogo aos vetores unitários da base. Na esfera unitária, todas as funções de quadrado integrável podem, portanto, ser expandidas como uma combinação linear de:

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,Y_{\ell }^{m}(\theta ,\varphi )}$. 

/G ψ = E ψ =  E [tG+].... ../ c .

Essa expansão é exata sempre que ${\displaystyle \ell }$ estende-se até o infinito. Haverá um erro de truncamento ao limitar a soma sobre ${\displaystyle \ell }$ numa largura de banda finita ${\displaystyle L}$. Os coeficientes da expansão ${\displaystyle f_{\ell }^{m}}$ podem ser obtidos multiplicando-se a equação pelo conjugado complexo dos harmónicos esféricos, integrando-se sobre um ângulo sólido ${\displaystyle \Omega \!\,}$ e usando-se as relações de ortogonalidade acima. No caso de harmónicos ortonormalizados, obtemos

${\displaystyle f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )d\Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \sin \theta f(\theta ,\varphi )Y_{\ell }^{m*}(\theta ,\varphi )}$.

/G ψ = E ψ =  E [tG+].... ../ c .

Um conjunto alternativo de harmónicos esféricos para funções reais pode ser obtido a partir do conjunto

${\displaystyle Y_{\ell m}={\begin{cases}Y_{\ell }^{0}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad {\mbox{ si }}m=0\\{1 \over {\sqrt {2}}}\left(Y_{\ell }^{m}+(-1)^{m}\,Y_{\ell }^{-m}\right)={\sqrt {2}}NP_{\ell }^{m}(\theta )\cos m\varphi \qquad \quad \quad {\mbox{si }}m>0\\{1 \over i{\sqrt {2}}}\left(Y_{\ell }^{|m|}-(-1)^{|m|}\,Y_{\ell }^{-|m|}\right)={\sqrt {2}}NP_{\ell }^{|m|}(\theta )\sin |m|\varphi \quad {\mbox{ si }}m<0.\end{cases}}}$

/G ψ = E ψ =  E [tG+].... ../ c .

Estas funções têm as mesmas propriedades que as funções de normalização complexas dadas anteriormente. Nesta forma, uma função real integrável pode ser expressa como uma soma infinita de harmónicos esféricos

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{lm}\,Y_{lm}(\theta ,\varphi )}$.

/G ψ = E ψ =  E [tG+].... ../ c .

Harmónicos esféricos em física

Seguem-se algumas aplicações dos harmónicos esféricos na física, tanto na eletrostática como na mecânica quântica.

Harmónicos esféricos na eletrostática

O átomo de hidrogênio

Ver artigo principal: Átomo de Hidrogênio

O modelo quântico moderno do átomo de hidrogênio assume o elétron em um estado constante de energia tem sua posição distribuída ao redor do núcleo atômico como uma distribuição de probabilidades, cuja variação angular é dada por um harmónico esférico.

Análise espectral

A potência total de uma função ${\displaystyle f}$ é definida na linguagem de processamento de sinais eletrônicos como sendo a integral do quadrado da função dividida pela área varrida por ela. Usando as propriedades de ortonormalização de funções harmónicas esféricas de potência real unitária, é fácil verificar que a potência total de uma função definida na esfera unitária está relacionada aos seus coeficientes espectrais através de uma generalização do teorema de Parseval:

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{l=0}^{\infty }S_{f\!f}(l)}$,

/G ψ = E ψ =  E [tG+].... ../ c .

onde

${\displaystyle S_{f\!f}(l)=\sum _{m=-l}^{l}f_{lm}^{2}}$

/G ψ = E ψ =  E [tG+].... ../ c .

é definido como o espectro de potência angular. Da mesma forma, pode-se definir a potência cruzada entre duas funções como

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g(\Omega )\,d\Omega =\sum _{l=0}^{\infty }S_{fg}(l)}$, 

/G ψ = E ψ =  E [tG+].... ../ c .

onde

${\displaystyle S_{fg}(l)=\sum _{m=-l}^{l}f_{lm}g_{lm}}$

/G ψ = E ψ =  E [tG+].... ../ c .

é definido como o espectro cruzado neste caso. Se as funções ${\displaystyle f}$ e ${\displaystyle g}$ possuem valor médio igual a zero (ou seja, com coeficientes espectrais ${\displaystyle f_{00}}$ e ${\displaystyle g_{00}}$ nulos), então ${\displaystyle S_{f\!f}(l)}$ e ${\displaystyle S_{fg}(l)}$ representam as contribuições para a variância e covariância da função para ${\displaystyle \ell }$, respectivamente. É comum que o espectro de potência cruzado seja aproximado por uma lei de potências do tipo

${\displaystyle S_{f\!f}(l)=C\,\ell ^{\beta }}$. 

/G ψ = E ψ =  E [tG+].... ../ c .

Quando ${\displaystyle \beta =0}$, o espectro é "branco", pois cada nível tem potências iguais. Quando ${\displaystyle \beta <0}$, o espectro é chamado de "vermelho", porque não há mais energia nos níveis mais baixos com comprimentos de onda mais longos do que nos níveis mais elevados. Finalmente, quando ${\displaystyle \beta >0}$, o espectro é chamado de "azul".

Teorema da adição

Um resultado matemático de grande interesse e utilidade é chamado teorema da adição para harmónicos esféricos. Se dois vetores r e r' tem coordenadas esféricas ${\displaystyle (r,\theta ,\varphi )}$ e ${\displaystyle (r',\theta ',\varphi ')}$, respectivamente, o ângulo ${\displaystyle \gamma }$ entre eles é dado pela expressão

${\displaystyle \cos \gamma =\cos \theta \cos \theta '+\sin \theta \sin \theta '\cos(\varphi -\varphi ')}$.

/G ψ = E ψ =  E [tG+].... ../ c .

O teorema da adição expressa um polinômio de Legendre de ordem ${\displaystyle l}$ no ângulo ${\displaystyle \gamma }$ em termos de produtos de dois harmónicos esféricos com coordenadas angulares ${\displaystyle (\theta ,\varphi )}$ e ${\displaystyle (\theta ',\varphi ')}$:

${\displaystyle P_{l}(\cos \gamma )={\frac {4\pi }{2l+1}}\sum _{m=-l}^{l}Y_{lm}^{*}(\theta ',\phi ')\,Y_{lm}(\theta ,\varphi )}$. /G ψ = E ψ =  E [tG+].... ../ c .

Esta expressão é válida tanto para harmónicos reais como complexos. Entretanto, deve-se ressaltar que a fórmula apresentada anteriormente é válida apenas para harmónicos esféricos ortonormalizados. Harmónicos de potência unitária são necessários para eliminar o fator ${\displaystyle 4\pi }$ da expressão anterior.

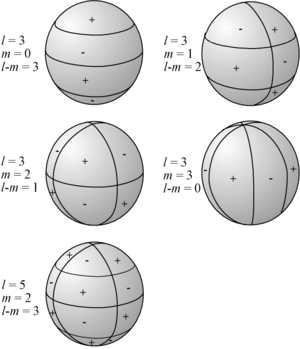
Visualizando os harmónicos esféricos

Representação esquemática de Y_lm sobre a esfera unitária. Y_lm é igual a 0 ao longo de m círculos que passam pelos polos e ao longo de l-m círculos de mesma latitude. A função muda de sinal cada vez que cruza uma dessas linhas.

A função harmónica esférica real Y₃₂ mostrada ao longo de quatro cortes.

/G ψ = E ψ =  E [tG+].... ../ c .

Os harmónicos esféricos são facilmente visualizados através da contagem do número de cruzamentos que ambos estão na direção das coordenadas ${\displaystyle \theta }$ e ${\displaystyle \varphi }$. Para obter a orientação sobre ${\displaystyle \theta }$, as funções associadas de Legendre possuem ${\displaystyle l-|m|}$ zeros, enquanto que na coordenada ${\displaystyle \varphi }$ as funções trigonométricas seno e cosseno possuem ${\displaystyle 2|m|}$ zeros.

Quando o harmónico esférico de ordem ${\displaystyle m}$ é nulo, as funções harmónicas esféricas não dependem de ${\displaystyle \varphi }$, e diz-se que a função é zonal. Quando ${\displaystyle l=|m|}$, não existem zeros na direção ${\displaystyle \theta }$, e diz-se que a função é setorial. Nos outros casos, as funções formam um padrão em xadrez sobre a esfera.

Expressões analíticas para os primeiros harmónicos esféricos

Eis as expressões analíticas dos primeiros harmónicos esféricos ortonormalizados, com a convenção de fase de Condon-Shortley:

${\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}$

${\displaystyle Y_{1}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{-i\varphi }}$

${\displaystyle Y_{1}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over \pi }}\,\cos \theta }$

${\displaystyle Y_{1}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{-2i\varphi }}$

${\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{-i\varphi }}$

${\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\,(3\cos ^{2}\theta -1)}$

${\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{2i\varphi }}$

${\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\,(5\cos ^{3}\theta -3\cos \theta )}$

/G ψ = E ψ =  E [tG+].... ../ c .

Ver também: [[:[[Tabela de harmónicos esféricos até Y₁₀]]]]